LA DILATACIÓN DE LOS CUERPOS
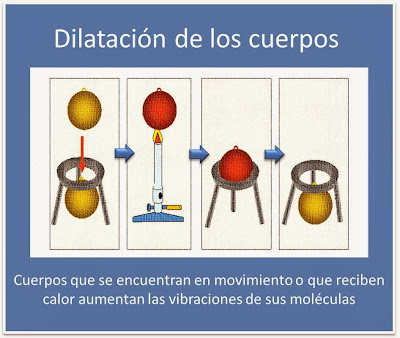
Los cuerpos que se encuentran en movimiento o que reciben calor aumentan las vibraciones de sus moléculas. Esto trae como consecuencia que exista un incremento en sus volúmenes, lo que se conoce como dilatación térmica.
La dilatación es un factor importante que se considera para la planificación de proyectos de ingeniería, como la construcción de puentes o edificios, entre otros. Por esta razón, es común ver en pistas y veredas unas pequeñas separaciones para evitar que se produzcan rompimientos cuando ganen calor y se dilaten.
La dilatación es el aumento de las dimensiones de los cuerpos, la cual depende del material del que están formados. Así, por ejemplo, el oro se dilata mucho más rápido que el vidrio. La dilatación puede ser lineal, superficial o cúbica.
DILATACIÓN LINEAL
La dilatación lineal es aquella en la cual predomina la variación en una única dimensión, o sea, en el ancho, largo o altura del cuerpo.
Para estudiar este tipo de dilatación, imaginemos una barra metálica de longitud inicial L0 y temperatura θ0.
Si calentamos esa barra hasta que la misma sufra una variación de temperatura Δθ, notaremos que su longitud pasa a ser igual a L (conforme podemos ver en la siguiente figura):

Matemáticamente podemos decir que la dilatación es:
 Pero si aumentamos el calentamiento, de forma de doblar la variación de temperatura, o sea, 2Δθ, entonces observaremos que la dilatación será el doble (2 ΔL).
Podemos concluir que la dilatación es directamente proporcional a la variación de temperatura.
Imaginemos dos barras del mismo material, pero de longitudes diferentes. Cuando calentamos estas barras, notaremos que la mayor se dilatará más que la menor.
Podemos concluir que, la dilatación es directamente proporcional al larco inicial de las barras.
Cuando calentamos igualmente dos barras de igual longitud, pero de materiales diferentes, notaremos que la dilatación será diferentes en las barras.
Pero si aumentamos el calentamiento, de forma de doblar la variación de temperatura, o sea, 2Δθ, entonces observaremos que la dilatación será el doble (2 ΔL).
Podemos concluir que la dilatación es directamente proporcional a la variación de temperatura.
Imaginemos dos barras del mismo material, pero de longitudes diferentes. Cuando calentamos estas barras, notaremos que la mayor se dilatará más que la menor.
Podemos concluir que, la dilatación es directamente proporcional al larco inicial de las barras.
Cuando calentamos igualmente dos barras de igual longitud, pero de materiales diferentes, notaremos que la dilatación será diferentes en las barras.
Podemos concluir que la dilatación depende del material (sustancia) de la barra.
De los ítems anteriores podemos escribir que la dilatación lineal es:

Donde:
L0 = longitud inicial.
L = longitud final.
ΔL = dilatación (DL > 0) ó contracción (DL < 0)
Δθ = θ0 – θ (variación de la temperatura)
α = es una constante de proporcionalidad característica del material que constituye la barra, denominada como coeficiente de dilatación térmica lineal.
De las ecuaciones I y II tendremos:
 La ecuación de la longitud final L = L0 (1 + α . Δθ), corresponde a una ecuación de 1º grado y por tanto, su gráfico será una recta inclinada, donde:
La ecuación de la longitud final L = L0 (1 + α . Δθ), corresponde a una ecuación de 1º grado y por tanto, su gráfico será una recta inclinada, donde:
L = f (θ) ==> L = L0 (1 + α . Δθ).

Observaciones:
Todos Los coeficientes de dilatación sean α, β ou γ, tienen como unidad:
(temperatura)-1 ==> ºC-1
DILATACIÓN SUPERFICIAL
Es aquella en que predomina la variación en dos dimensiones, o sea, la variación del área del cuerpo
Para estudiar este tipo de dilatación, podemos imaginar una placa metálica de área inicial S0 y temperatura inicial θ0. Si la calentáramos hasta la temperatura final θ, su área pasará a tener un valor final igual a S.

La dilatación superficial ocurre de forma análoga a la de la dilatación lineal; por tanto podemos obtener las siguientes ecuaciones:


Lee todo en: Dilatación Lineal, Superficial y Volumétrica | La guía de Física http://fisica.laguia2000.com/fisica-del-estado-solido/dilatacion-lineal-superficial-y-volumetrica#ixzz4PIoURIdR
Pero si aumentamos el calentamiento, de forma de doblar la variación de temperatura, o sea, 2Δθ, entonces observaremos que la dilatación será el doble (2 ΔL).
Podemos concluir que la dilatación es directamente proporcional a la variación de temperatura.
Imaginemos dos barras del mismo material, pero de longitudes diferentes. Cuando calentamos estas barras, notaremos que la mayor se dilatará más que la menor.
Podemos concluir que, la dilatación es directamente proporcional al larco inicial de las barras.
Cuando calentamos igualmente dos barras de igual longitud, pero de materiales diferentes, notaremos que la dilatación será diferentes en las barras.
Podemos concluir que la dilatación depende del material (sustancia) de la barra.
Podemos concluir que la dilatación depende del material (sustancia) de la barra.
De los ítems anteriores podemos escribir que la dilatación lineal es:
Donde:
L0 = longitud inicial.
L = longitud final.
ΔL = dilatación (DL > 0) ó contracción (DL < 0)
Δθ = θ0 – θ (variación de la temperatura)
De las ecuaciones I y II tendremos:
Observaciones:
Todos Los coeficientes de dilatación sean α, β ou γ, tienen como unidad:
Todos Los coeficientes de dilatación sean α, β ou γ, tienen como unidad:
(temperatura)-1 ==> ºC-1
DILATACIÓN SUPERFICIAL
Es aquella en que predomina la variación en dos dimensiones, o sea, la variación del área del cuerpo
Para estudiar este tipo de dilatación, podemos imaginar una placa metálica de área inicial S0 y temperatura inicial θ0. Si la calentáramos hasta la temperatura final θ, su área pasará a tener un valor final igual a S.
La dilatación superficial ocurre de forma análoga a la de la dilatación lineal; por tanto podemos obtener las siguientes ecuaciones:
Lee todo en: Dilatación Lineal, Superficial y Volumétrica | La guía de Física http://fisica.laguia2000.com/fisica-del-estado-solido/dilatacion-lineal-superficial-y-volumetrica#ixzz4PIoURIdR
Un tema muy interesante y con bastantes aplicaciones. :)
ResponderBorrar